If you apply the matrix to the vector
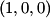 you get you get 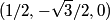 which means that the matrix rotates vectors which means that the matrix rotates vectors 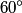 clockwise about the clockwise about the  axis. We are told that both axis. We are told that both 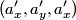 and and 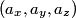 represent the same vector. Therefore, the reference frame represent the same vector. Therefore, the reference frame 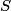 must be rotated must be rotated 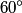 counterclockwise about the counterclockwise about the  axis so that axis so that 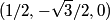 represents the same vector as represents the same vector as 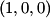 in the initial reference frame. Therefore, answer (E) is correct. in the initial reference frame. Therefore, answer (E) is correct. |